UJI KRUSKAL WALLIS
KONSEP DASAR UJI KRUSKAL WALLIS
Uji Kruskal-Wallis adalah salah satu metode statistik nonparametrik yang digunakan untuk menguji perbedaan rata-rata di antara tiga kelompok atau lebih yang independen. Uji ini sering digunakan ketika data tidak memenuhi asumsi normalitas atau homogenitas varians yang diperlukan oleh uji parametrik seperti Uji ANOVA. Dalam analisis data dengan SPSS, Uji Kruskal-Wallis adalah alat yang berguna untuk menguji perbedaan di antara kelompok-kelompok yang tidak terdistribusi secara normal.
Uji Kruskal-Wallis adalah metode statistik nonparametrik yang memiliki kelebihan dan kekurangan yang perlu dipertimbangkan. Berikut adalah penjelasan mengenai kelebihan dan kekurangan Uji Kruskal-Wallis.
Berikut Kelebihan Uji Kruskal-Wallis, diantaranya:
- Tidak memerlukan asumsi distribusi normal: Uji Kruskal-Wallis tidak bergantung pada asumsi distribusi normal pada data. Oleh karena itu, uji ini dapat digunakan dengan aman pada data yang tidak terdistribusi secara normal atau memiliki outlier yang signifikan.
- Tahan terhadap perbedaan varians: Uji Kruskal-Wallis juga tidak memerlukan asumsi homogenitas varians antara kelompok-kelompok yang dibandingkan. Dengan demikian, uji ini dapat digunakan ketika varians antara kelompok-kelompok tidak sama atau tidak dapat diasumsikan sama.
- Sensitif terhadap perbedaan peringkat: Uji Kruskal-Wallis menggunakan peringkat data, bukan nilai aktual, dalam analisis. Oleh karena itu, uji ini mampu mendeteksi perbedaan yang signifikan jika terdapat perbedaan dalam peringkat data di antara kelompok-kelompok yang diuji.
- Fleksibilitas dalam analisis data: Uji Kruskal-Wallis dapat digunakan untuk menguji perbedaan di antara tiga kelompok atau lebih. Hal ini memberikan fleksibilitas dalam analisis data yang melibatkan lebih dari dua kelompok.
Selain memiliki kelebihan, Uji Kruskal Wallis juga memiliki kekurangan, diantaranya :
- Tidak memberikan informasi tentang kelompok yang berbeda secara spesifik: Meskipun Uji Kruskal-Wallis dapat mengindikasikan adanya perbedaan yang signifikan di antara kelompok-kelompok yang diuji, uji ini tidak memberikan informasi spesifik tentang kelompok mana yang berbeda secara signifikan. Untuk mengetahui perbedaan antara kelompok secara spesifik, diperlukan analisis lanjutan seperti uji pasangan atau kontras.
- Tidak dapat mengatasi data yang terstruktur dengan baik: Uji Kruskal-Wallis bekerja dengan baik pada data yang tidak terstruktur atau tidak memiliki pola tertentu. Namun, jika data memiliki struktur atau pola tertentu, seperti pengukuran berulang atau desain terkendali, uji ini mungkin tidak memberikan hasil yang akurat atau relevan.
- Sensitivitas terhadap jumlah data yang sedikit: Uji Kruskal-Wallis cenderung menjadi kurang sensitif ketika sampel dalam kelompok yang dibandingkan terlalu kecil. Dalam kasus ini, kesalahan jenis II (mengabaikan perbedaan yang sebenarnya) dapat terjadi.
- Tidak dapat memberikan estimasi parameter populasi: Uji Kruskal-Wallis hanya memberikan informasi tentang adanya perbedaan yang signifikan di antara kelompok-kelompok yang diuji, tetapi tidak memberikan estimasi tentang parameter populasi seperti rata-rata atau proporsi. Oleh karena itu, uji ini tidak memberikan informasi mengenai ukuran efek atau perbedaan.
Contoh kasus yang digunakan dalam tulisan ini adalah dimana seorang peneliti ingin mengetahui apakah ada perbedaan signifikan penjualan suatu produk A di 3 kota dengan menggunakan alpha 5%. Untuk menjawab hal tersebut, peneliti menggunakan uji Kruskal Wallis dengan harapan data yang digunakan juga tidak berdistribusi normal, agar penggunaan uji Kruskal Wallis bisa dilakukan.
BERIKUT CARA UJI KRUSKAL WALLIS DI SPSS:
- Siapkan tabulasi data di Excel, lalu input data atau masukan data ke SPSS pada Page Data View.
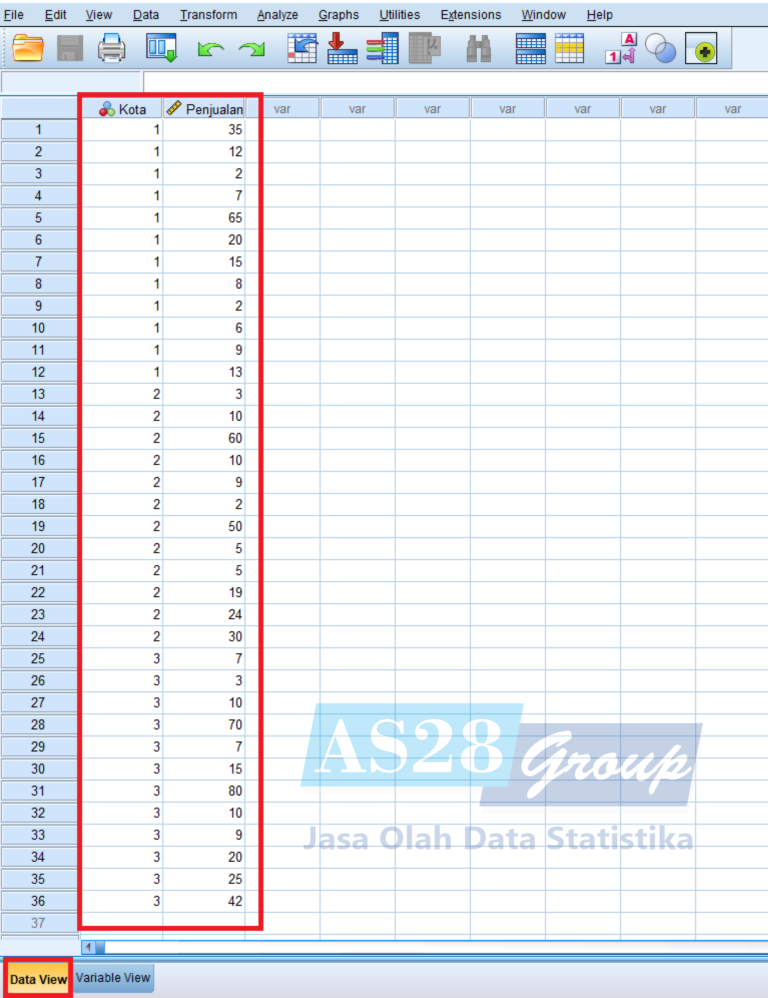
- Jangan lupa isikan juga pada Page Variable View.

- Isikan juga pada Value Label di Variabel Kelompok. Value 1 untuk Kota A, Value 2 untuk Kota B dan Value 3 untuk Kota C, lalu pilih OK.
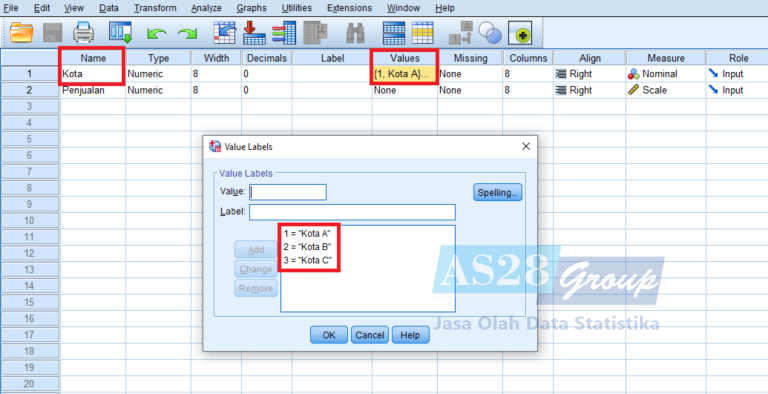
- Selanjutnya melakukan Uji Normalitas, dengan cara pilih Analyze – Descriptive Statistics – Explore.
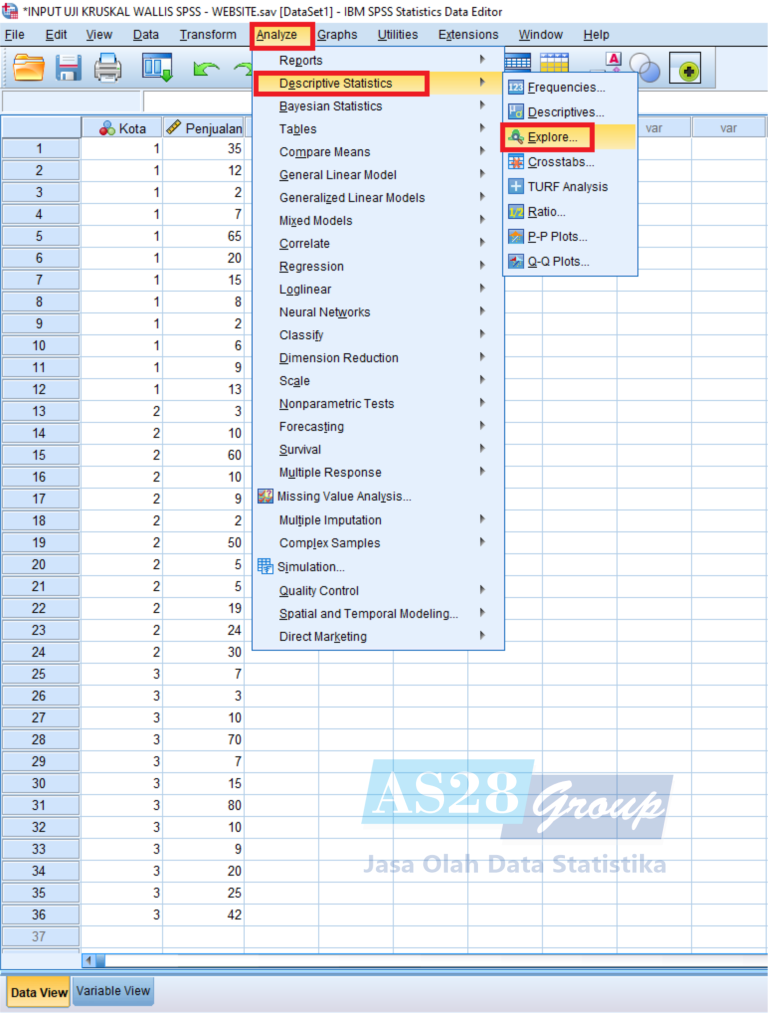
- Muncul kotak dialog Uji Normalitas, seperti ini :
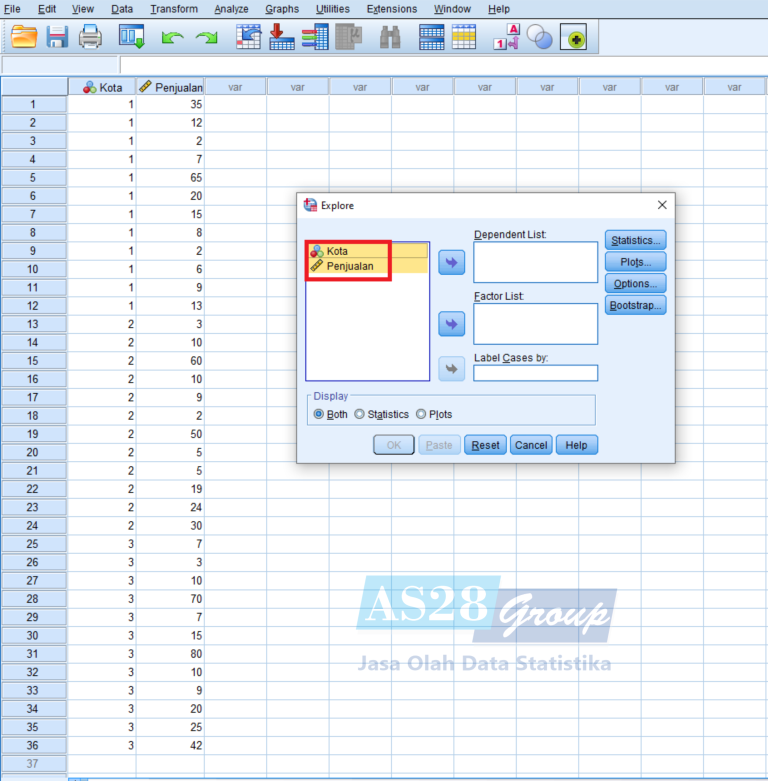
- Muncul kotak dialog Uji Normalitas, seperti ini :
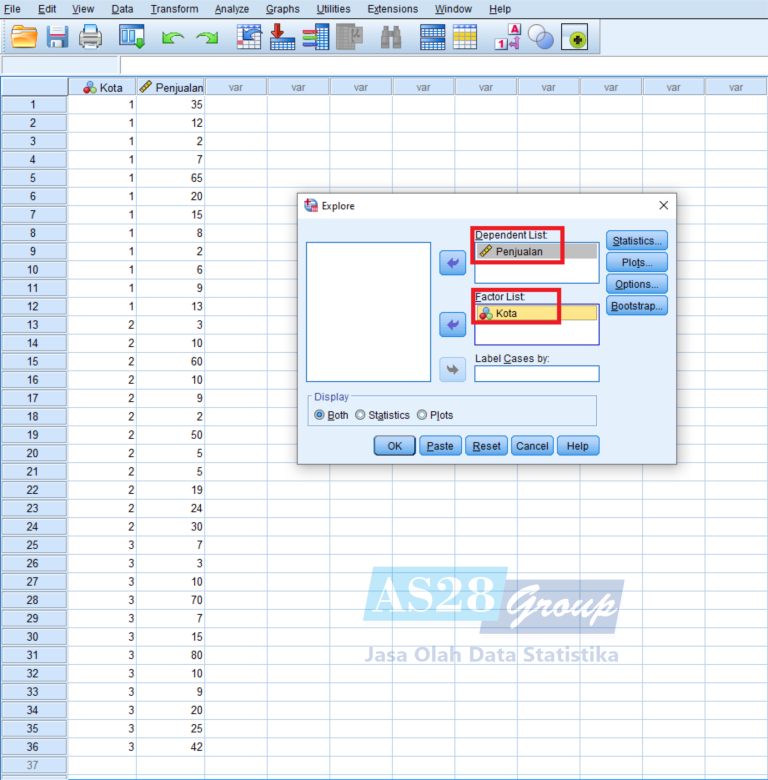
- Selanjutnya pilih Plots, Ceklis Normality Plots With Test lalu pilih Continue dan OK.
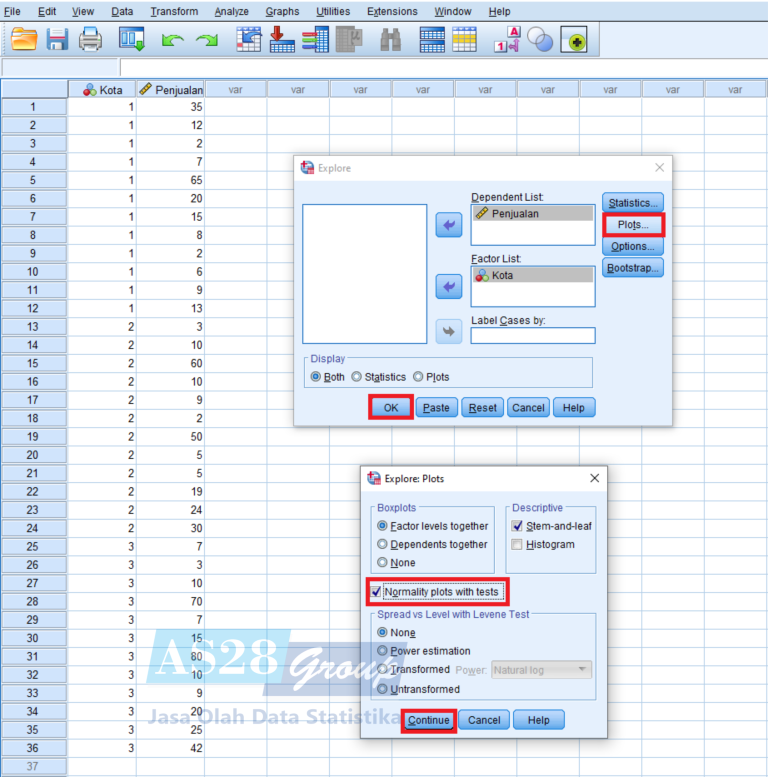
- Keluar Output SPSS untuk Uji Normalitas :
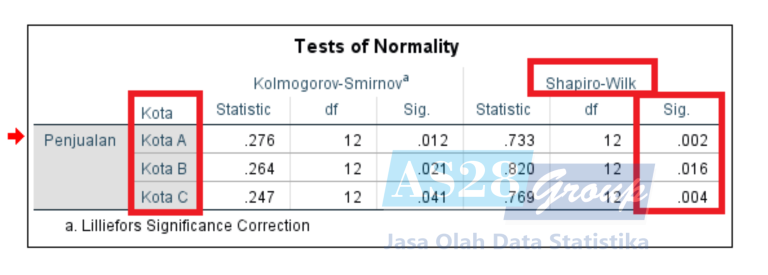
- Kriteria Pengujian Uji Normalitas :
- Nilai Shapiro Wilk > 0.05 berkesimpulan Data berdistribusi Normal atau asumsi Uji Normalitas terpenuhi.
- Nilai Shapiro Wilk < 0.05 berkesimpulan Data berdistribusi tidak Normal atau asumsi Uji Normalitas tidak terpenuhi.
- Interpretasi Output Uji Normalitas :
Diketahui nilai Sig. Shapiro Wilk Variabel Kota A sebesar 0.002 (<0.05), Kota B sebesar 0.016 (<0.05) dan Variabel Kota C sebesar 0.004 (<0.05) maka bisa disimpulkan bahwa data yang digunakan (Kota A, B dan C) tidak berdistribusi normal dengan kata lain asumsi uji normalitas tidak terpenuhi. Penggunaan uji normalitas shapiro wilk dikarenakan jumlah data yang dipakai kurang dari 50 (<50). Setelah mengetahui bahwasanya asumsi normalitas data tidak terpenuhi, maka bisa lanjut ke Uji Kruskal Wallis.
- Selanjutnya melakukan Uji Kruskal Wallis, dengan cara pilih Analyze – Nonparametric Test – Legacy Dialogs – K Independent Samples
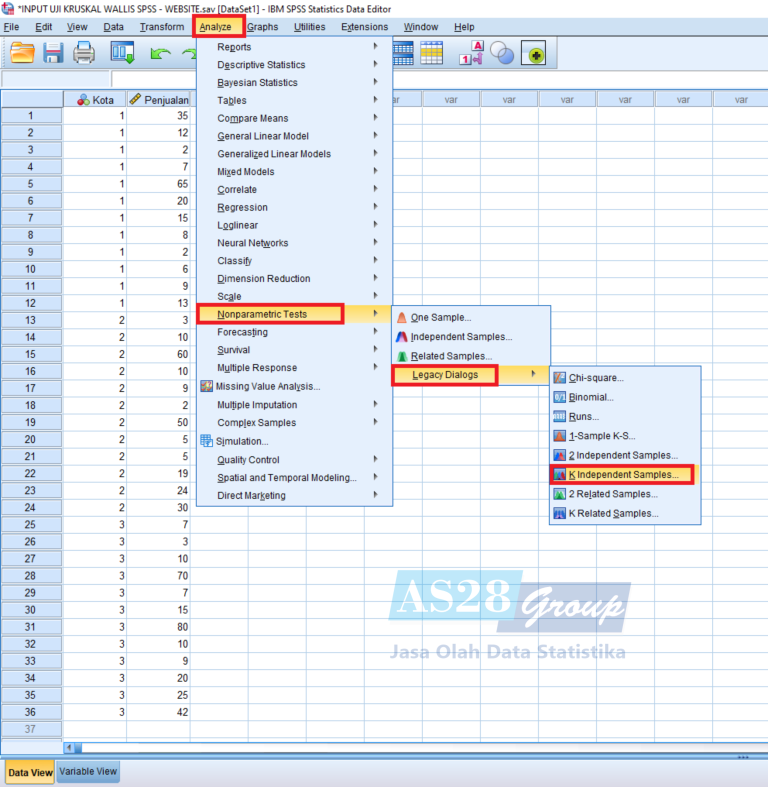
- Muncul kotak dialog Uji Kruskal Wallis, seperti ini :
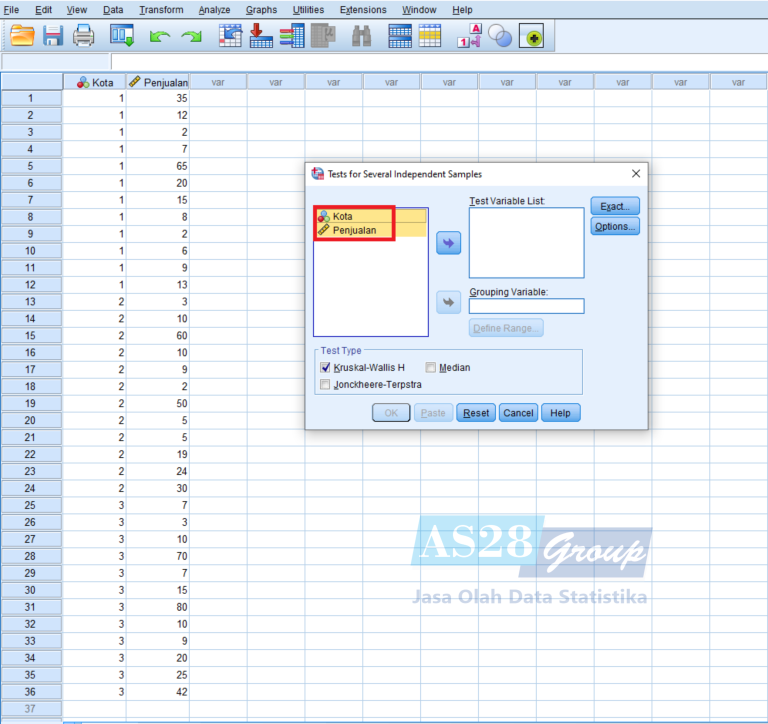
- Masukan Variabel Penjualan ke kolom Test Variable List, lalu Kota ke Grouping Variable.

- Masukan Variabel Penjualan ke kolom Test Variable List, lalu Kota ke Grouping Variable.
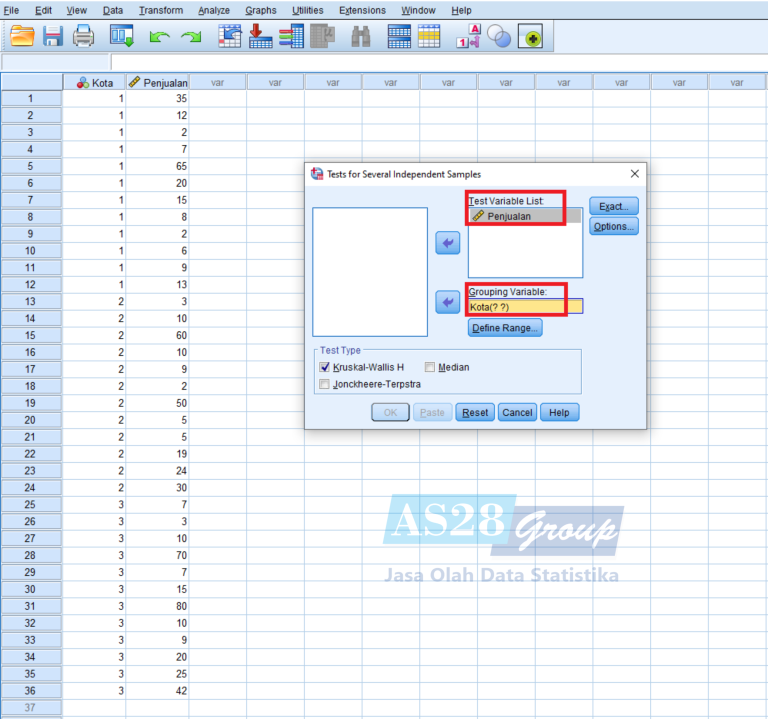
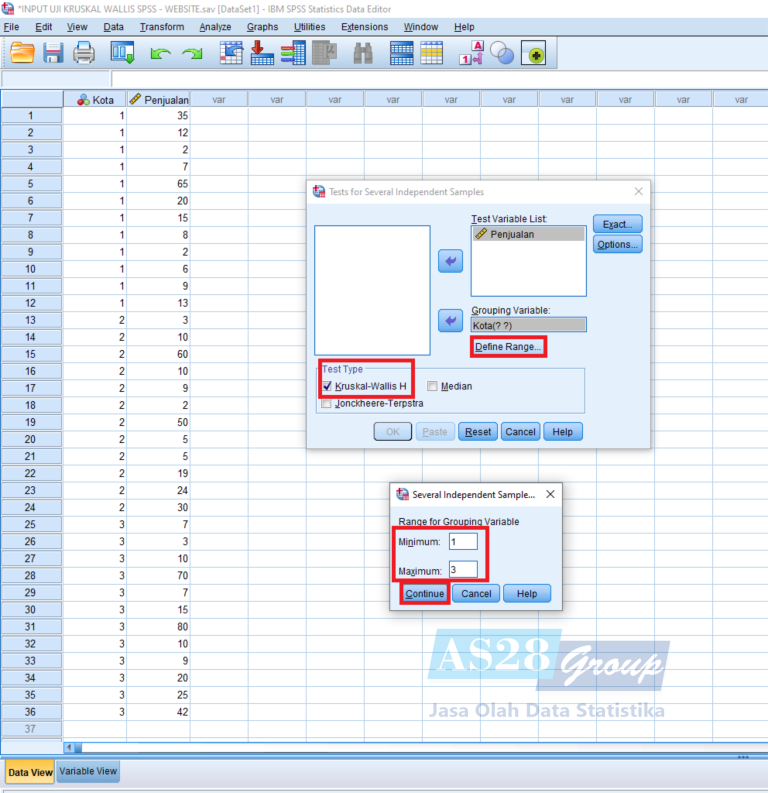
- Selanjutnya pilih Define Range, isikan angka 1 pada kolom Minimum dan angka 3 pada kolom Maximum, dikarenakan ada 3 kelompok yang akan di analisis, lalu Continue dan OK.
- Keluar Output SPSS untuk Uji Kruskal Wallis
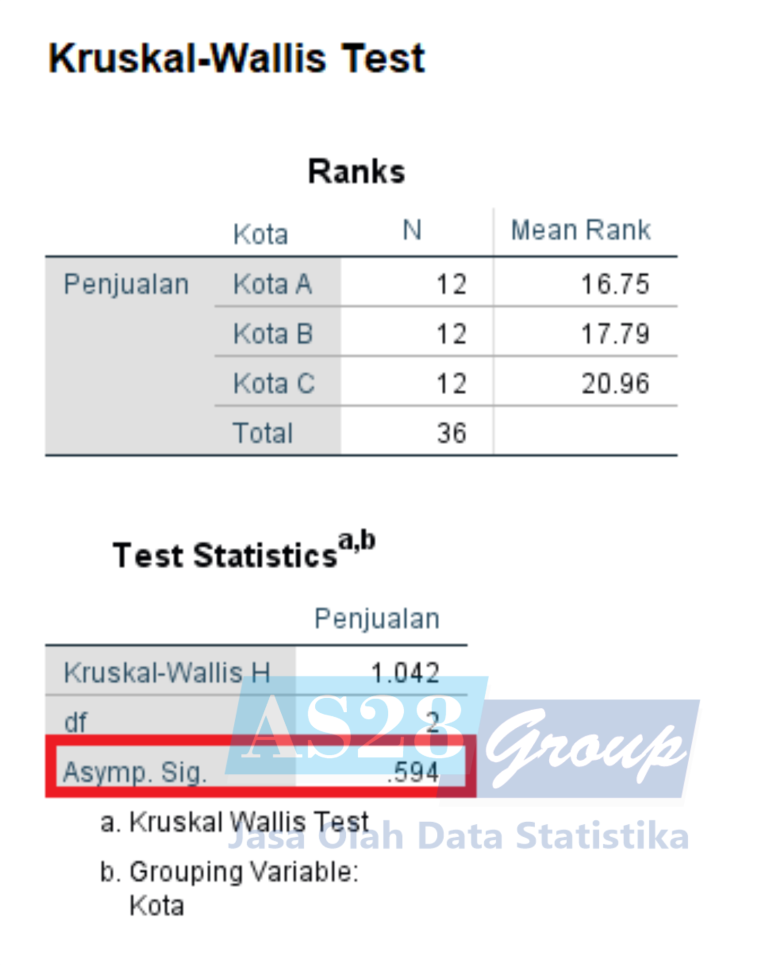
- Kriteria Pengujian Uji Kruskal Wallis :
- Nilai Sig > 0.05 berkesimpulan Tidak ada perbedaan secara signifikan.
- Nilai Sig < 0.05 berkesimpulan Ada perbedaan secara signifikan.
- Interpretasi Output Uji Kruskal Wallis :
Diketahui nilai Asymp. Sig sebesar 0.594 (>0.05) maka bisa disimpulkan bahwa tidak ada perbedaan secara signifikan antar 3 kelompok atau tidak ada perbedaan secara signifikan penjualan produk A di 3 kota.